A 21st Century Clavichord:
Exploring Clavichords as Precedent Studies for the Design of a Modern Portable Keyboard Instrument
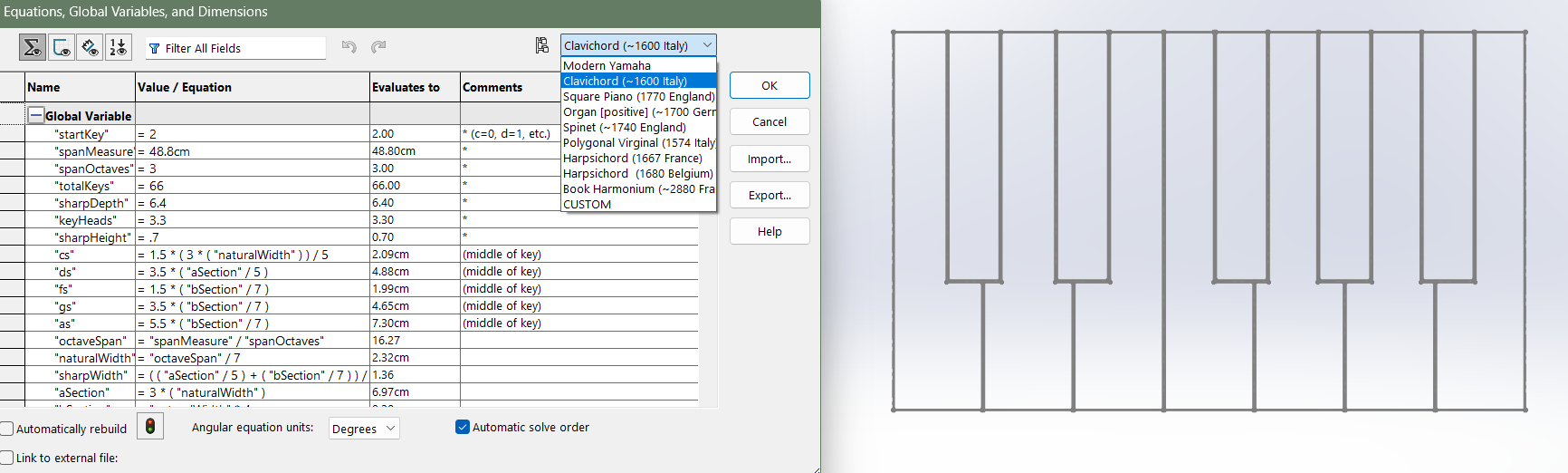
Mathematically Defining a Keyboard Layout
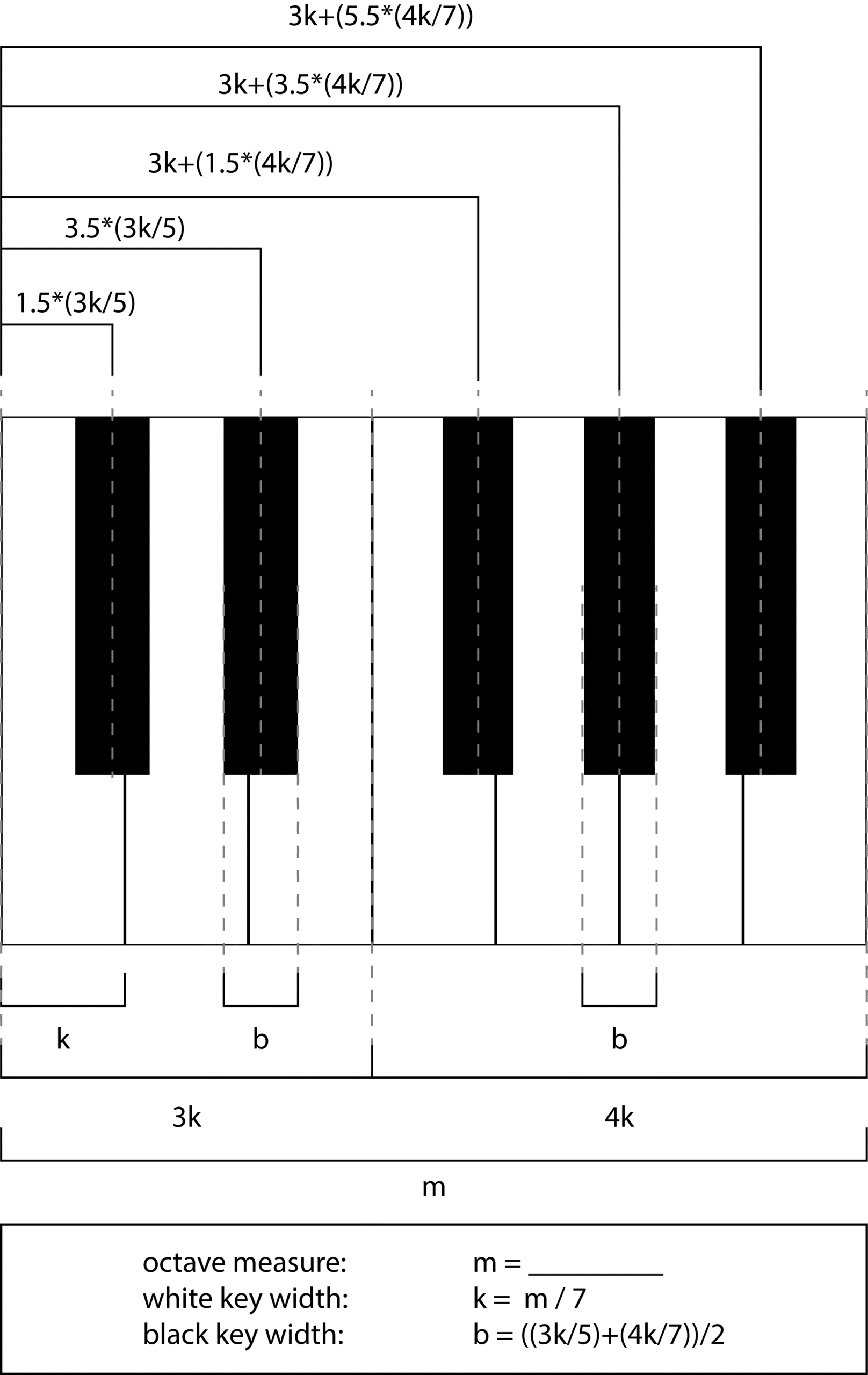
The horizontal dimensions of the keyboard are derived from the octave measure .The octave is divided evenly into 7 white key heads with widths of . To determine the placements and width of the black keys, we must look at the octave in two sections: C-E (three white keys, two black), and F-B (four white keys, 3 black).
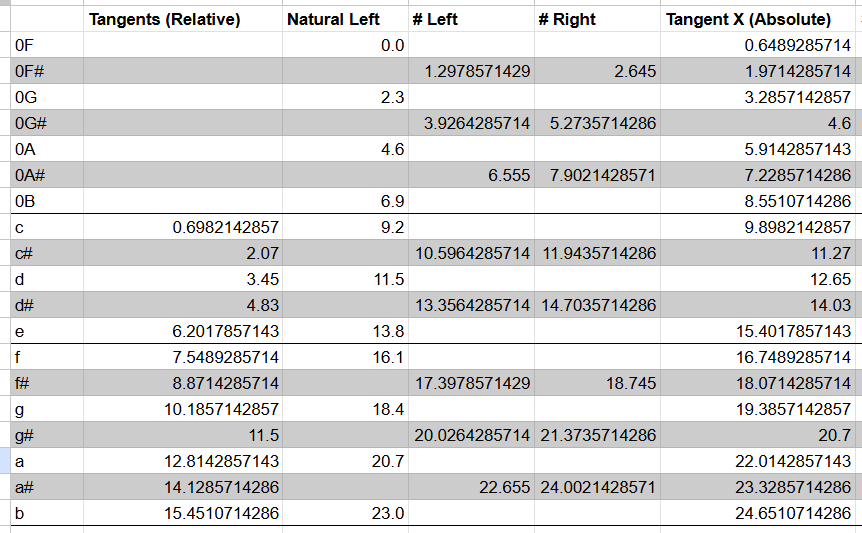
Starting with the later section we can find the centerlines of the black keys. If we divide the C-E span into 5 segments (for the five total keys) the two black keys will be centered within the second and fourth segments. This gives the horizontal locations of the centers of C# and D# in relation to the left edge of the octave as and respectively. The centers of the black keys in the second section can be calculated similarly by dividing the width of the F-B span into seven segments. As the locations are in relation to the left edge of the octave, the width of the C-E needs to be added. This gives F# a center at , G# at , and A# at .
The width of the black keys is the average of the widths of the two sections’ segments . The edges of the black keys can then be determined by adding or subtracting from their centerline, for example, the left edge of C# is at .
The exact calculations for the centerlines (of the back edge) of the white keys differ between notes but is the average of the right edge of the previous note and the left edge of the next. Two examples are as follows: